Special Systems

Banded, LU, and Cholesky

Advanced factorization techniques for efficiency and speed.

🎯 Lecture Goals

1 Review Tridiagonal and Banded systems.
2 Understand LU Decomposition.
3 Master Cholesky Factorization ($LL^T$).

Tridiagonal Systems

\[ A = \begin{bmatrix} d_1 & c_1 & & & \\ a_1 & d_2 & c_2 & & \\ & a_2 & d_3 & c_3 & \\ & & \ddots & \ddots & \ddots \\ & & & a_{n-1} & d_n \end{bmatrix} \]

Efficiency

Storage: Only $3n-2$ entries vs $n^2$. No need to store zeros!
Speed: Operations can be saved.

Elimination Algorithm

for i = 2:n
    xmult = a(i-1) / d(i-1)
    d(i) = d(i) - xmult * c(i-1)
    b(i) = b(i) - xmult * b(i-1)
end

Cost: $\mathcal{O}(n)$

Banded Systems

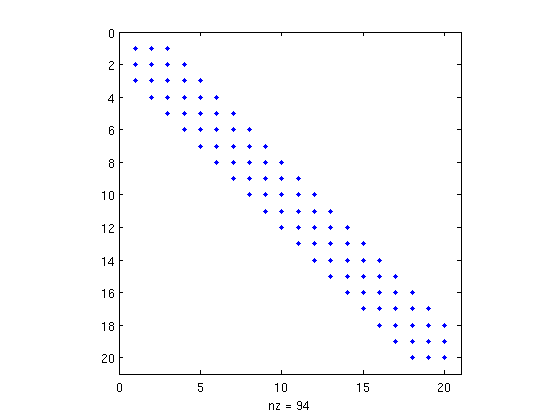
Bandwidth $m=5$

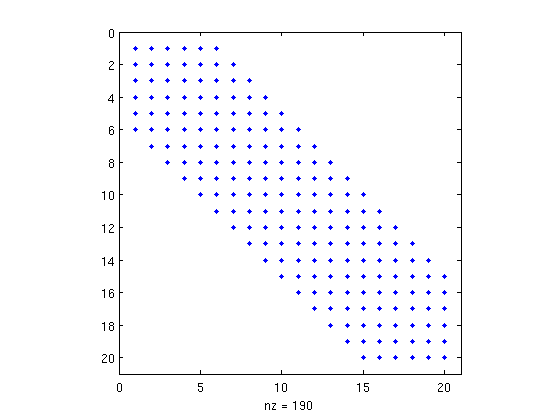
Bandwidth $m=11$

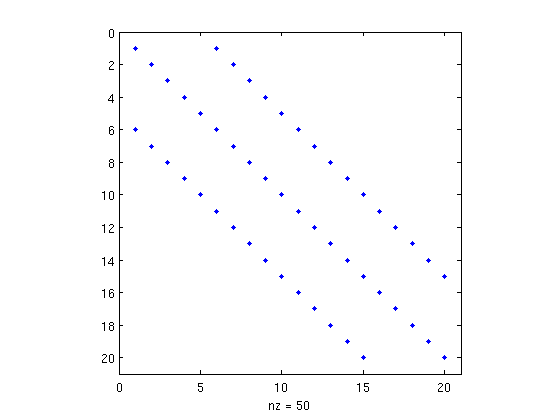
Fill-in

Fill-in: During Gaussian Elimination, zeros inside the band can become non-zeros.

Cost for $m$-band system: $\mathcal{O}(m^2 n)$.

Motivation: Graph Theory

Example Graph Structure

➜

\[ \begin{bmatrix} 2 & -1 & 0 & 0 & -1 & 0 \\ -1 & 3 & -1 & 0 & -1 & 0 \\ 0 & -1 & 2 & 0 & -1 & 0 \\ 0 & 0 & -1 & 3 & -1 & -1 \\ -1 & -1 & 0 & -1 & 3 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{bmatrix} \]

Graph Laplacian Matrix

Why Factorize?

Graph problems often require solving $Ax=b$ for many different $b$ vectors.

Gaussian Elimination (for $k$ vectors): $\mO(k n^3)$
LU Decomposition (solve $k$ times): $\mO(n^3 + k n^2)$

LU Decomposition

Factorize $A$ into Lower ($L$) and Upper ($U$) triangular matrices: $A = LU$.

The Solve Process

1. Factorize
$A \to L, U$

2. Forward Solve
$Ly = b$

3. Backward Solve
$Ux = y$

With Pivoting

With pivoting, we get $PA = LU$, where $P$ is a permutation matrix.

                    % MATLAB
                    [L, U, P] = lu(A);
                    y = L \ (P * b);
                    x = U \ y;
                

Cholesky Factorization ($LL^T$)

Requirements

Matrix $A$ must be:

Symmetric: $A = A^T$
Positive Definite (SPD): $x^T A x > 0$ for all $x \ne 0$.

Advantages

Half the FLOPS: Only calculate $L$.
Memory Efficient: Save 50% storage.
Stable: No pivoting required! Elements of $L$ do not grow excessively.
Fast: Usually >2x faster than LU.

Algorithm

for k = 1:n
    L(k,k) = sqrt(A(k,k) - sum(L(k, 1:k-1).^2));
    for j = k+1:n
        L(j,k) = (A(j,k) - sum(L(j,1:k-1).*L(k,1:k-1))) / L(k,k);
    end
end

The Backslash Operator (\)

In MATLAB, x = A \ b is smart!

1. Is $A$ Triangular? $\to$ Substitution.

2. Is $A$ Symmetric Positive Definite? $\to$ Cholesky.

3. Is $A$ Square? $\to$ LU Factorization.

4. Not Square? $\to$ QR Factorization (Least Squares).

🧠 Final Challenge +20 XP

Why is Cholesky factorization preferred over LU factorization for Symmetric Positive Definite (SPD) matrices?