Lecture 1

Introduction to Numerical Methods

1

Numerical vs. Symbolic Calculation

Numerical Calculation

Involves numbers directly. Manipulates numbers to produce a numerical result.

\[ \frac{(17.36)^2 - 1}{17.36 + 1} = 16.36 \]

Symbolic Calculation

Symbols represent numbers. Manipulates symbols according to mathematical rules to produce a symbolic result.

\[ \frac{x^2 - 1}{x + 1} = x-1 \]

Analytic Solution

The exact numerical or symbolic representation of the solution. May use special characters such as $\pi$, $e$, or $\tan(83)$.

$\frac{1}{4}$
$\pi$
$\frac{1}{3}$
$\tan(83)$

Numerical Solution

The computational representation of the solution. Entirely numerical.

$0.25$
$3.14159\dots(?)$
$0.33333\dots(?)$
$0.88472\dots(?)$

Numerical Computation and Approximation

Numerical Approximation is needed to carry out steps in numerical calculation.

Symbolic Computation, Numerical Solution

\[ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} - 1 = \frac{1}{12} = 0.0833\dots \]

Numerical Computation, Numerical Approximation

\[ 0.500 + 0.333 + 0.250 - 1.000 = 0.083 \]
2

Core Concepts

Method vs. Algorithm vs. Implementation

  • METHOD A general (mathematical) framework describing the solution process. Is it a "good" method?
  • ALGORITHM A detailed description of executing the method. Is it a robust algorithm?
  • IMPLEMENTATION A particular instantiation of the algorithm. Is it a fast implementation?

The Big Theme: Trade-offs

Figure showing pull towards Accuracy Accuracy
💰
Cost
3

History of Numerical Algorithms

Rhind Papyrus

Rhind Papyrus (1650 BC)

Ancient Egypt. Contains 85 problems. Approximates $\pi$ with $(8/9)^2 * 4 \approx 3.1605$.

Archimedes

Archimedes (287-212 BC)

"Method of Exhaustion". Determined $\frac{223}{71} < \pi < \frac{22}{7}$ (3.1408 < $\pi$ < 3.1429).

Method of Exhaustion:

  • A circle is a polygon with infinite sides.
  • $C_n$ = circumference of n-sided polygon.
  • $\lim_{n\rightarrow\infty} C_n = \pi$.
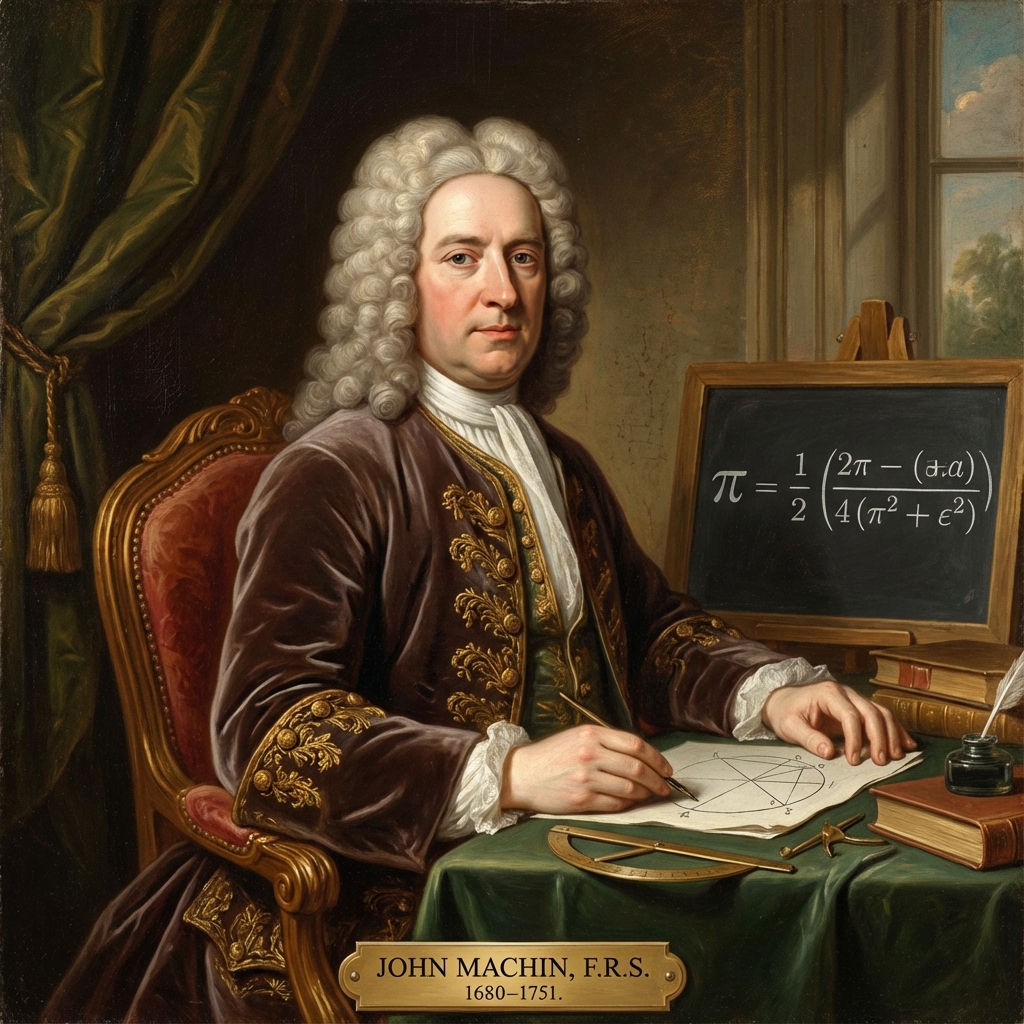
John Machin

John Machin (1700)

$\pi = 16 \arctan(\frac{1}{5}) - 4\arctan(\frac{1}{239})$.
Calculated first 100 digits of $\pi$.

Numerical Analysis

"Study of algorithms for the problems of continuous mathematics"

— Trefethen

The Big Questions

  • How algorithms work and how they fail
  • Why algorithms work and why they fail

Numerical Focus

Approximation
How close is the solution?
Efficiency
How fast and cheap?
Stability
Sensitivity to small variations?
Error
Role of finite precision?

⚠️ Real World Impact: Failures

  • Patriot Missile (1991): Rounding errors resulted in failure to intercept, 28 deaths.
  • Ariane 5 Rocket (1996): Integer overflow caused explosion just after lift-off.
  • Sleipner A Platform (1991): Inaccurate finite element analysis caused sinking ($1 Billion loss).
💻

CS Connections

AI (Transitions, Patterns) Informatics (Google Matrix) Graphics (Compression, Lighting) Security (Random Numbers) Finance (Monte Carlo)
4

Taylor Series Approximation

Computers can only add and multiply. They can't directly evaluate $e^x$, $\cos(x)$, or $\sqrt{x}$. We use Taylor Series approximations.

The Taylor Series

\[ f(x) = \sum_{k=0}^{\infty} \frac{(x-c)^{k}}{k!} f^{(k)}(c) \]

Example: $e^x$ (at $c=0$)

\[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots \]

We can't evaluate infinite terms, so we truncate to a polynomial $p_n(x)$.

Evaluation of $e^2$:

  • $p_0(2) = 1$ (Poor fit)
  • $p_1(2) = 1 + 2 = 3$ (Better)
  • $p_2(2) = 1 + 2 + 2 = 5$ (Good fit)

Error Analysis

\[ f(x) = p_n(x) + E_n(x) \]

Where the error term is:

\[ E_n(x) = \frac{(x-c)^{n+1}}{(n+1)!}f^{(n+1)}(\xi) = \mO(h^{n+1}) \]

assuming $h = x-c$

Truncation Error Example: $\sin(x)$

If $x \ll 1$, remaining terms are small ($x^7/7! \dots$).

\[ \sin(x) = \underbrace{x - \frac{x^3}{3!} + \frac{x^5}{5!}}_{\text{approx}} \underbrace{- \frac{x^7}{7!} + \dots}_{\text{truncation error}} \]

🧠 Knowledge Check +10 XP

If we approximate $e^x$ using the first 3 terms ($1 + x + x^2/2$), what is the order of the error term?

Process Implementation

Typical process to find $f'(x)$ using definition: $f'(x) = \lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h}$

Pseudo Code

h = 1
x = 1
for i = 1 to 20 do
  h = h / 2
  y = (f(x+h) - f(x)) / h
  err = |f'(x) - y|
end

Matlab

f = inline('exp(x)');
h = 1;
x = 1;
for i = 1:20
  h = h / 2;
  y = (f(x+h) - f(x)) / h;
  err(i) = abs(f(x) - y);
end

Types of Error

Absolute Error:
$|x_{true} - x_{approx}|$
Relative Error:
$\left|\frac{x_{true} - x_{approx}}{x_{true}}\right|$
Interactive Computing
5

Interactive Playground

Experiment with the algorithms below. You can run MATLAB code via Octave Online or Python code directly in your browser.

Octave MATLAB / Octave (Online)

Copy & Paste into Terminal:

🚀 Open Octave Online

Python Python (Client-Side)

Output
Loading Python environment...