Rootfinding
Bisection, Newton's Method, and Convergence Analysis.
Motivation
Not all problems are linear systems ($Ax=b$). Many real-world problems require solving non-linear equations $f(x)=0$.
Examples
- Where should wireless access points be placed?
- Where do two curved surfaces intersect?
- What is the subsurface geology in a basin?
The Solution Strategy
We cannot always find a closed-form solution. Instead, we iterate, getting closer to the answer with each step.
Problem Statement
Given a function $f(x)$, find $x$ such that $f(x) = 0$.
Bracketing Methods
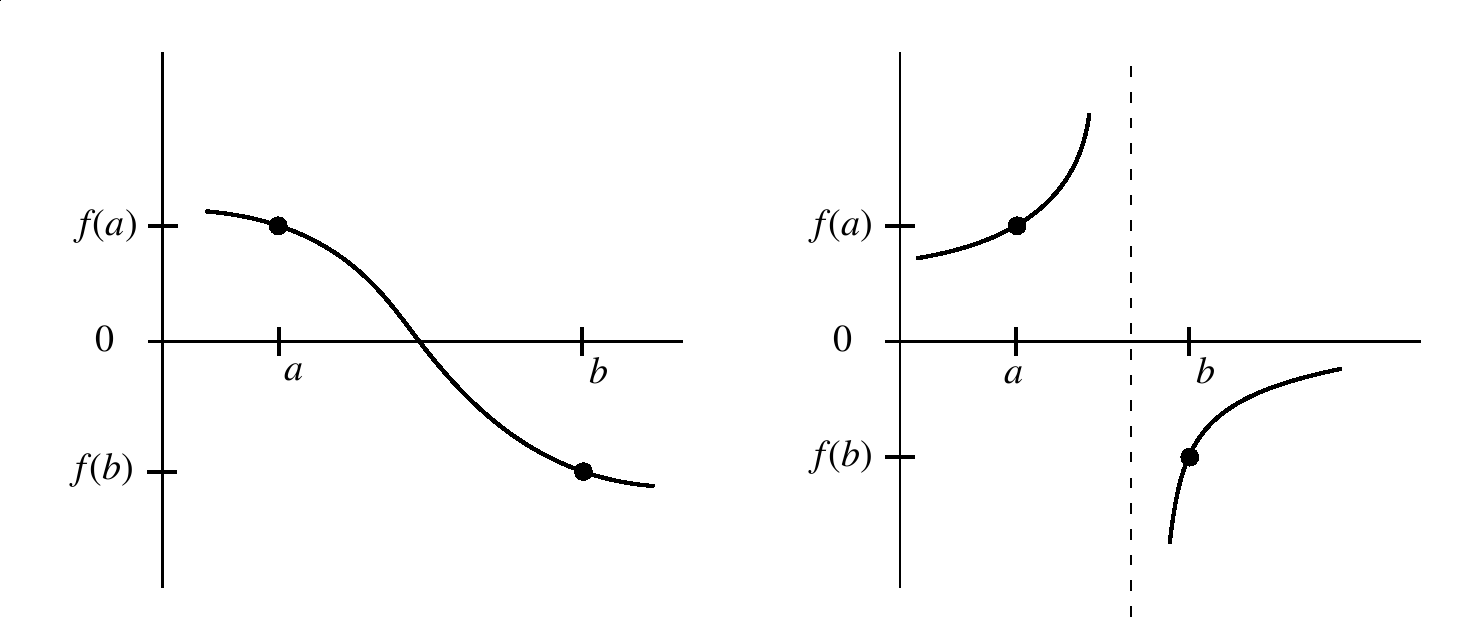
Concept
A root is bracketed on interval $[a,b]$ if $f(a)$ and $f(b)$ have opposite signs.
Root exists in [a, b]
Note: Use `sign()` instead of multiplication to avoid underflow.
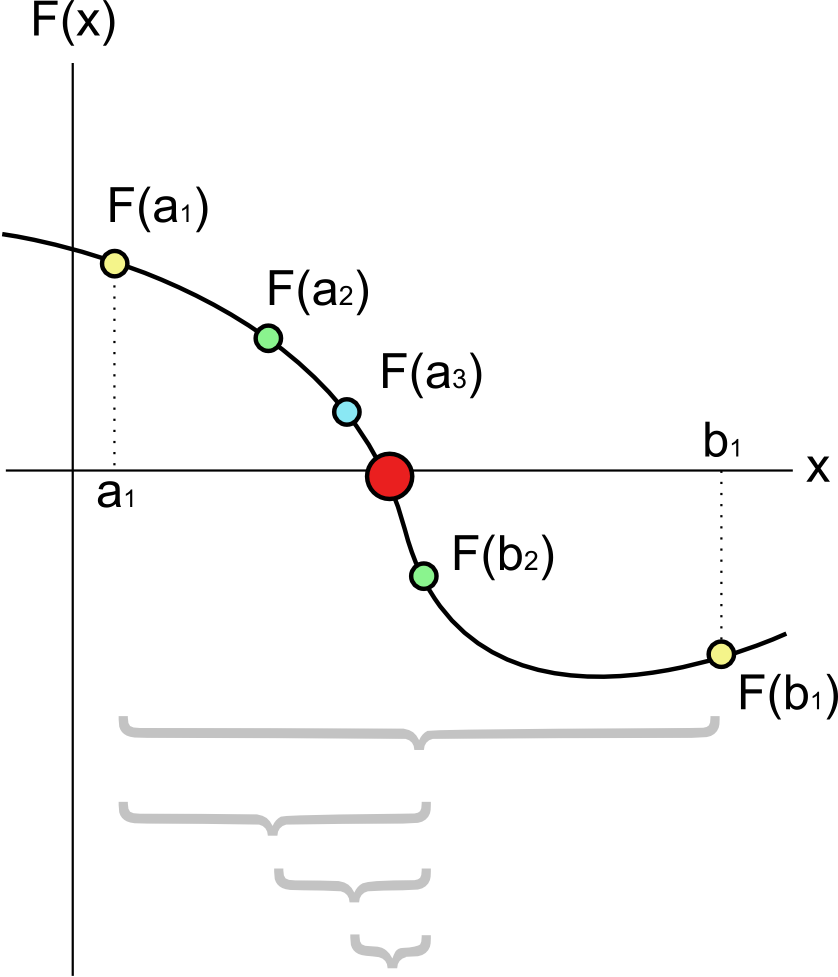
The Bisection Method
Given a bracket, halve the interval while keeping the root inside.
- Calculate midpoint: $x_m = a + (b-a)/2$
- Check sign of $f(x_m)$.
- Update bracket: if sign matches $f(a)$, set $a = x_m$, else $b = x_m$.
- Repeat.
Convergence Analysis
The interval size halves at each step: $\frac{\delta_n}{\delta_0} = 2^{-n}$.
Linear Convergence: Adds roughly 1 bit of accuracy per iteration (slow but reliable).
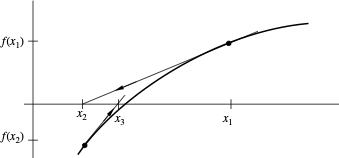
Newton's Method
Uses the slope (derivative) $f'(x)$ to project a tangent line to the x-axis for the next guess.
$x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}$
Comparison
| Method | Convergence | Pros | Cons |
|---|---|---|---|
| Bisection | Linear | Guaranteed to converge if bracketed. | Slow. |
| Newton | Quadratic | Extremely fast near root. | Needs $f'(x)$. Can diverge. |
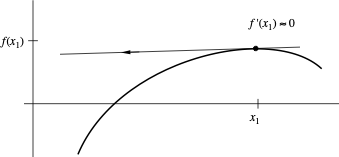
When Newton Fails
If $f'(x_k) \approx 0$ (tangent is horizontal), the next guess shoots off to infinity.
Convergence Criteria
How do we know when to stop?
Check $x$ (Step Size)
|x_k - x_{k-1}| < \delta_x
Good when function is steep.

Check $f(x)$ (Residual)
|f(x_k)| < \delta_f
Good when function is flat.

Division without Division
How do computers compute $1/q$ without using division? They use Newton's Method to find the root of a function where limit point is $1/q$, using only subtraction and multiplication.
Reciprocal Approximation Derivation
We want $x = 1/q$. This is the root of $f(x) = \frac{1}{x} - q = 0$.
Newton's Iteration:
This iteration converges quadratically to $1/q$ using only subtraction and multiplication!
Example: Compute $1/3$ ($q=3$)
Bracket: $1/4 < 1/3 < 1/2$. Let initial guess $x_0=1/4$.
- $x_0 = 1/4$
- $x_1 = 2(1/4) - 3(1/4)^2 = 1/2 - 3/16 = \mathbf{5/16}$
- $x_2 = 2(5/16) - 3(5/16)^2 = 160/256 - 75/256 = \mathbf{85/256}$
- $x_3 = 2(85/256) - 3(85/256)^2 = \mathbf{21845/65536}$
In just 3 steps, we have computed 16 bits of precision for $1/3$.
🧠 Final Challenge +20 XP
Why is Newton's Method considered to have "Quadratic Convergence"?