1. Introduction
Slides 2-3What is Numerical Analysis?
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to general symbolic manipulations) for problems of mathematical analysis.
"This does not require a very precise calculation. Sometimes the key point is to solve the problems with a (relatively) quick-and-dirty way, comparing to a full analytical solution."
1.1 Historical Context
Slides 4-5Historical Example: Babylonian Tablet

Dated 1800-1600 BC. Approximation of $\sqrt{2}$:
$$1 + 24/60 + 51/60^2 + 10/60^3$$
$= 1.41421296...$
Modern Context
"The real speciality of computers is repetition." Your computer can perform boring calculations millions of times. A smarter way provides quick and precise results.
2. The Art of Music 🎵
Slides 6-12Converting audio to sheet music involves analyzing frequencies.
Generating/Loading Audio (A440 Hz)
2.1 Fourier Analysis
Slides 10-12Fourier Transform (Spectrum)
We use the Fast Fourier Transform (FFT) to find the dominant frequencies.
Result: A sharp peak at 440 Hz is expected!
3. Errors in Computation ⚠️
Slides 24-26The Calculator Experiment
If you pick a calculator, insert a number, and press $\sqrt{}$ many times, you reach "1". Then square it back... you might not get the original number.
Types of Errors
1. Blunders / Bugs
Typographical errors, wrong data files, human error.
2. Roundoff Errors
Floating point numbers have finite precision.
4. Floating Point Arithmetic 💻
Slides 27-30IEEE 754 Standard
4.1 IEEE 754 Visualized
Slides 27-30 (Cont.)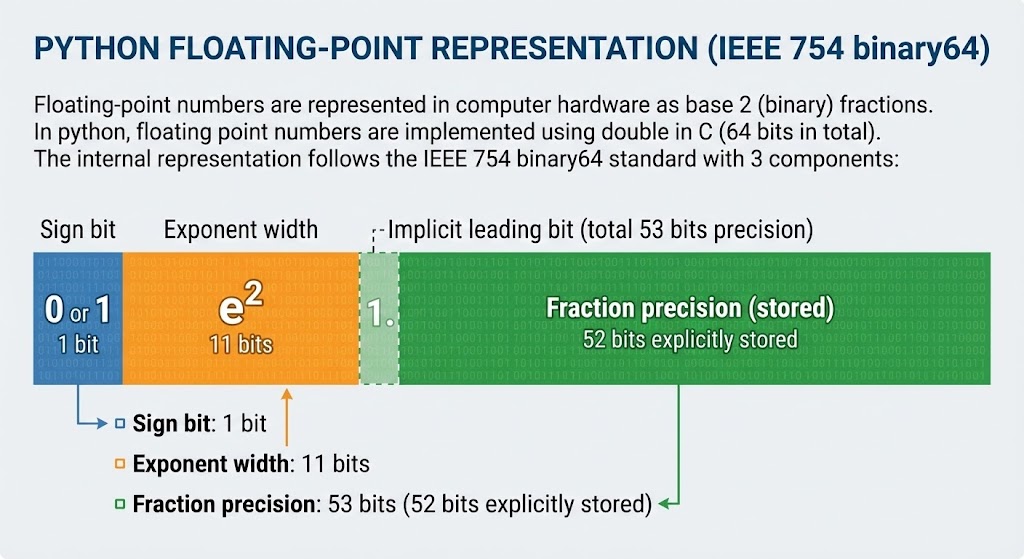
4.2 Video Reference 🎥
Video4.3 Precision Issues
Slides 27-30 (Cont.)"The Spoon is Not Real"
Computers cannot represent 0.1 exactly.
4.4 Lecture Video 🎥
Video5. Calculating $\pi$ 🥧
Slides 32-37Using polygon approximation. As the number of sides $N$ increases, precision SHOULD improve, but eventually degrades due to roundoff.
What goes wrong?
For very large $N$, $S$ becomes very small. $4 - S^2$ hits the limit of double precision, causing Catastrophic Cancellation.