1. The Scenario
The Setup
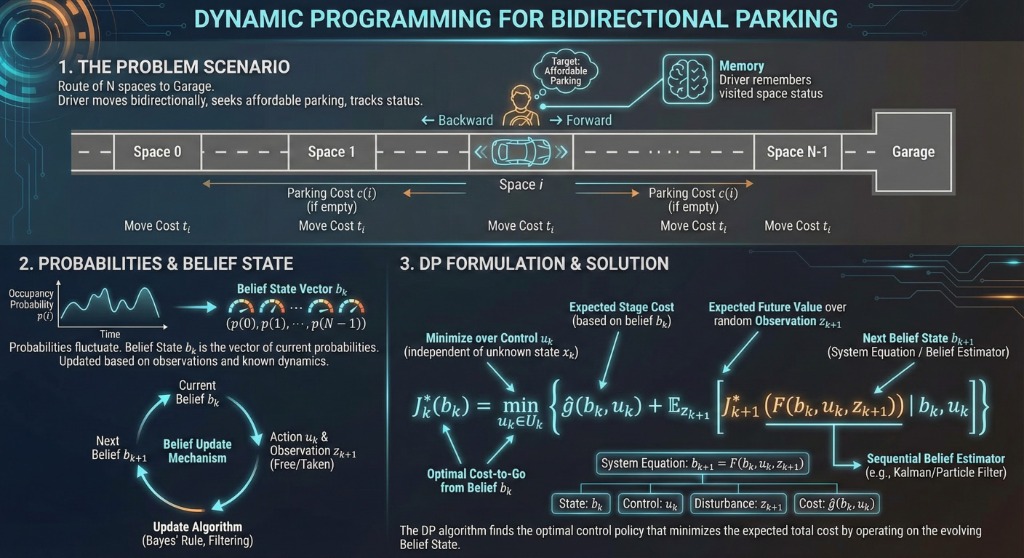
- Line of \(N\) parking spaces ending in a Garage.
- Driver can move Forward or Backward.
- Cost \(c(i)\) to park at space \(i\).
- Movement cost \(t_i\) between adjacent spaces.
Memory & Uncertainty
- Driver remembers status of visited spaces.
- Occupancy probability \(p(i)\) fluctuates over time.
- Status may change between visits!
2. Dynamics & Belief State
Since probabilities change, we need to track the Belief State.
Belief State \(b_k\)
The vector of current probabilities for all spaces:
\[ b_k = (p(0), p(1), \dots, p(N-1)) \]
Update Mechanism: At each step, the belief state is updated based on:
1. The known dynamics (e.g., probability increases by a factor).
2. The latest observation (Free/Taken) if a space is visited.
3. DP Formulation
Bellman Equation for Belief State
\[ J^*_k(b_k) = \min_{u_k \in U_k} \left\{ \hat{g}(b_k, u_k) + E_{z_{k+1}} \left[ J^*_{k+1} \left( F(b_k, u_k, z_{k+1}) \right) \mid b_k, u_k \right] \right\} \]\(J^*_k(b_k)\): Optimal cost-to-go from belief \(b_k\).
\(\hat{g}(b_k, u_k)\): Expected stage cost.
\(F(b_k, u_k, z_{k+1})\): Sequential Belief Estimator (System Equation).
\(z_{k+1}\): Random observation (Disturbance).
4. Beyond Single Agent

Image Source: Wikipedia (Fair Use)
Multiagent Systems
What if there are multiple drivers? Or multiple robots like Wall-E working together?
This leads to Multiagent Problems and Multiagent Rollout, where agents must coordinate their decisions.
Watch Wall-E Trailer