Nonlinear Equations

Bisection & Newton's Method

Algorithms for finding roots of functions.

The Bisection Method

Concept

Given a bracketed root (interval $[a,b]$ where $f(a)$ and $f(b)$ have opposite signs), split the bracket in half. Select the sub-bracket that contains the root. Repeat.

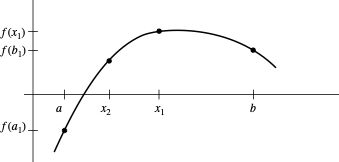
Algorithm

% Bisection
initialize a, b
for k = 1, 2, ...
    x_m = a + (b - a) / 2
    if sign(f(x_m)) == sign(f(a))
        a = x_m
    else
        b = x_m
    end
    if converged, stop
    end

Analysis

Interval size reduces by half each step: $\delta_n = 2^{-n} \delta_0$.

Linear Convergence: $n = \log_2(\frac{\delta_n}{\delta_0})$. To reduce error by $10^{-3}$, need $\approx 10$ steps.

Bisection Example

Solve $x - x^{1/3} - 2 = 0$. Initial bracket $[3, 4]$.

k	a	b	$x_{mid}$	$f(x_{mid})$
0	3	4	-	-
1	3	4	3.5	-0.018
2	3.5	4	3.75	0.196
3	3.5	3.75	3.625	0.089

Convergence Criteria

Check Step Size ($x$)

$|x_k - x_{k-1}| < \delta_x

Best when $f'(x)$ is large.

Check Function Value ($f(x)$)

$|f(x_k)| < \delta_f$

Best when $f'(x)$ is small.

Newton's Method

Use the slope $f'(x_k)$ to predict where the function crosses zero. Derived from Taylor Series.

$x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}$

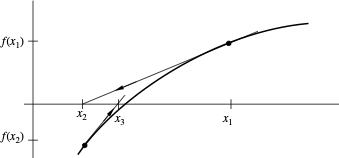
Example Comparison

Solve $x - x^{1/3} - 2 = 0$.

k	$x_k$	$f(x_k)$
0	3	-0.442
1	3.5266	0.0045
2	3.5213	$3.7 \times 10^{-7}$
3	3.5213	$2.6 \times 10^{-15}$

Converged in 3 steps! (vs ~50 for bisection)

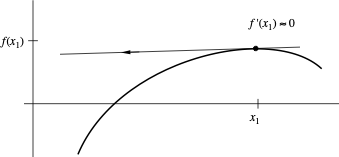
When Newton Fails

If $f'(x_k) \approx 0$, the next guess shoots off to infinity.

Secant Method

What if we don't know $f'(x)$? Approximate it using the last two points.

$x_{k+1} = x_k - f(x_k) \frac{x_k - x_{k-1}}{f(x_k) - f(x_{k-1})}$

Pros

No derivative needed.
Fast convergence ($r \approx 1.62$).

Cons

Needs two initial guesses.
Not guaranteed to bracket.
Can diverge.

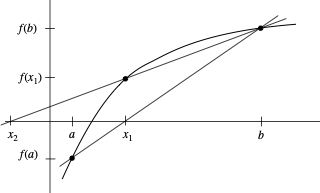
Summary & MATLAB's fzero

Bisection: Robust, slow, needs bracket.

Newton: Fast (Quadratic), needs derivative, can diverge.

Secant: Fast (Superlinear), no derivative, needs 2 guesses.

MATLAB: fzero

Hybrid method! Combines Bisection, Secant, and Inverse Quadratic Interpolation.

options = optimset('Display','iter');
x = fzero(@(x) x^10 - 1, 0.5, options);

🧠 Final Challenge +20 XP

Which method would you choose if you need guaranteed convergence and have a valid bracket, even if it's slow?