Gauss Quadrature
Optimal node placement for maximum precision integration.
Recap: Newton-Cotes
Previously, we used equally spaced nodes (Trapezoid, Simpson). This is restrictive and prone to oscillation (Runge's phenomenon).
Trapezoid (n=1): 2 points, exact for degree 1.
Simpson (n=2): 3 points, exact for degree 3.
Gaussian Quadrature Idea
What if we choose the nodes ($x_j$) optimally instead of fixing them?
Degrees of Freedom
With $n+1$ points, we have $n+1$ weights ($w_j$) AND $n+1$ locations ($x_j$).
Total unknowns = $2n+2$.
Result: Exact integration for polynomials of degree $2n+1$.
Deriving the 2-Point Rule
Let's find the best 2 points ($x_0, x_1$) and weights ($w_0, w_1$) for $\int_{-1}^1 f(x) dx$.
Equations (Exact for $1, x, x^2, x^3$)
- $w_0 + w_1 = \int_{-1}^1 1 dx = 2$
- $w_0x_0 + w_1x_1 = \int_{-1}^1 x dx = 0$
- $w_0x_0^2 + w_1x_1^2 = \int_{-1}^1 x^2 dx = 2/3$
- $w_0x_0^3 + w_1x_1^3 = \int_{-1}^1 x^3 dx = 0$
Solution
$w_0 = 1, \quad w_1 = 1$
$x_0 = -\frac{1}{\sqrt{3}}, \quad x_1 = \frac{1}{\sqrt{3}}$
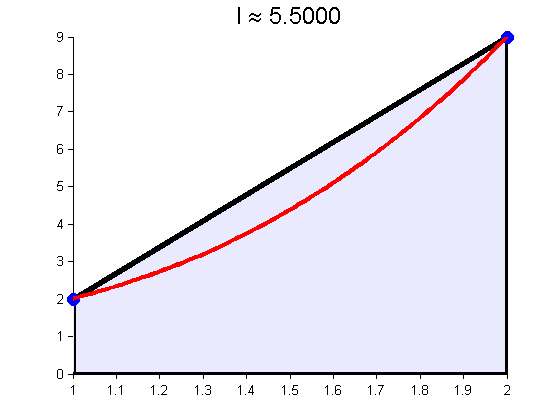
Trapezoid (End Points)
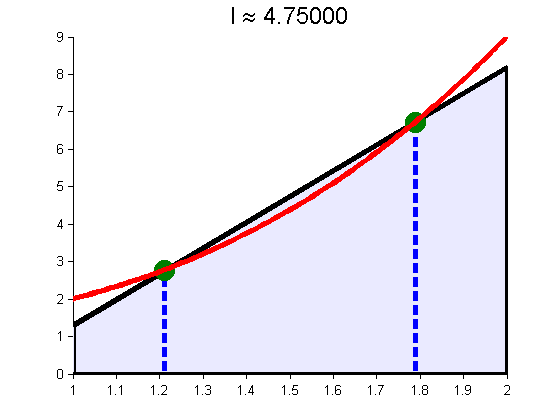
Gauss (Interior Points)
General Theory
The optimal nodes $x_j$ are the roots of Legendre Polynomials.
Legendre Polynomials
- $P_0(x) = 1$
- $P_1(x) = x$
- $P_2(x) = \frac{3x^2-1}{2}$ (Roots $\pm 1/\sqrt{3}$)
- $P_3(x) = \frac{5x^3-3x}{2}$ (Roots $0, \pm \sqrt{3/5}$)
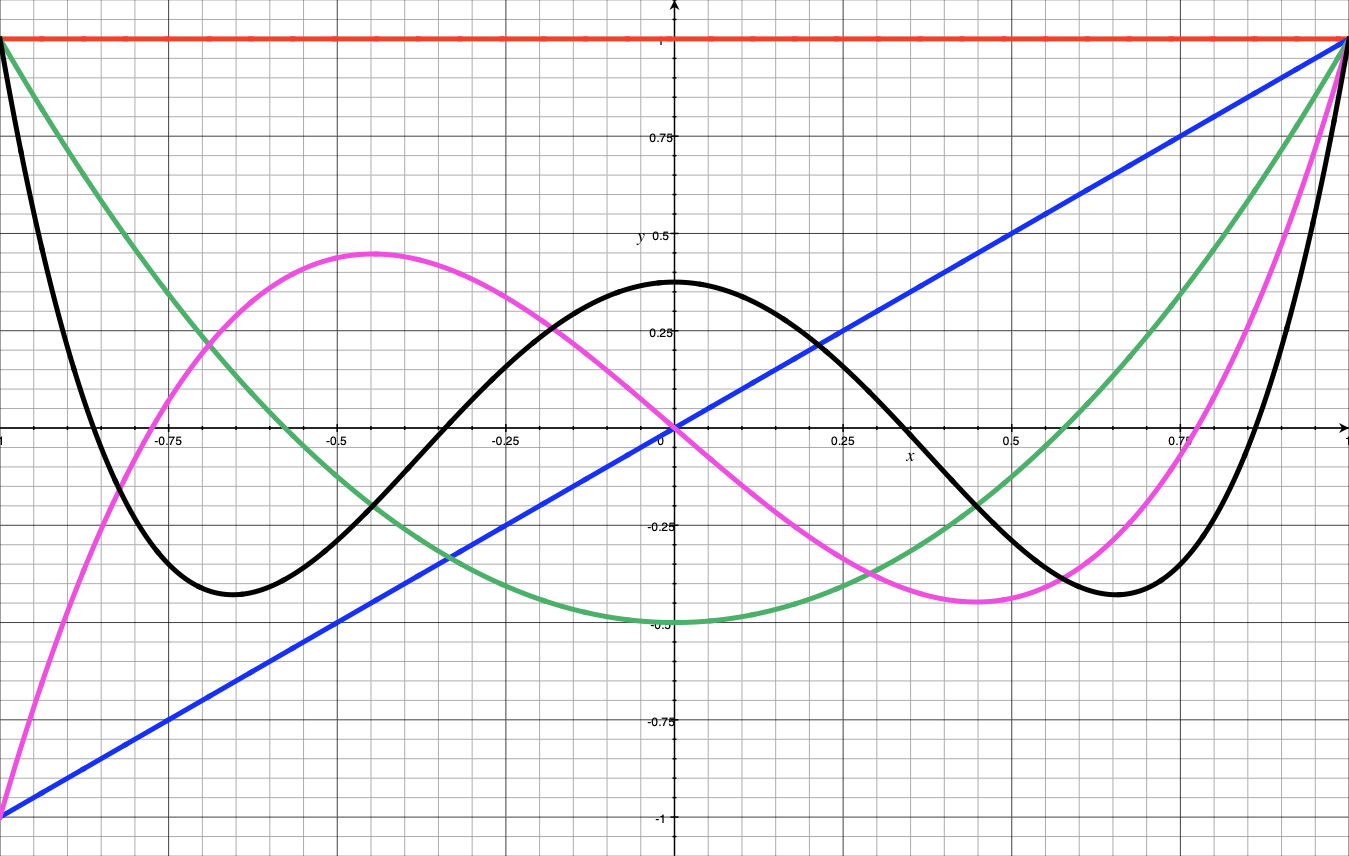
Roots are the nodes.

Nodes cluster towards the endpoints (like Chebyshev).
Using Gauss Quadrature
Gauss rules are defined for $\int_{-1}^1$. To integrate over $[a,b]$, we must change variables.
Transformation Formula
$\int_a^b f(x) dx = \frac{b-a}{2} \int_{-1}^1 f\left( \frac{b-a}{2}t + \frac{b+a}{2} \right) dt$
Example: $\int_0^1 x^2 e^{-x} dx$ ($n=1$, 2 points)
1. Map $[0,1]$ to $[-1,1]$: $x = \frac{1}{2}(t+1)$, $dx = \frac{1}{2} dt$.
2. Integral becomes $\frac{1}{2} \int_{-1}^1 (\frac{t+1}{2})^2 e^{-(t+1)/2} dt$.
3. Evaluate at $t = \pm 1/\sqrt{3}$ with weights 1.
Result $\approx 0.1594$
🧠 Knowledge Check +20 XP
How many points ($n+1$) does Gauss Quadrature need to exactly integrate a polynomial of degree 5?
Real World: Finite Elements
In Finite Element Analysis (FEA), we integrate functions over millions of 3D elements (tetrahedrons/bricks). Minimizing function evaluations is critical.
Gauss Quadrature is standard here.