Newton-Cotes Integration
Approximating integrals when antiderivatives are unknown.
Introduction
Why Numerical Integration?
- Often $f(x)$ is only known at discrete points (data).
- The antiderivative $F(x)$ may not exist in closed form (e.g., $e^{-x^2}$).
- We need to compute integrals quickly for real-time applications.
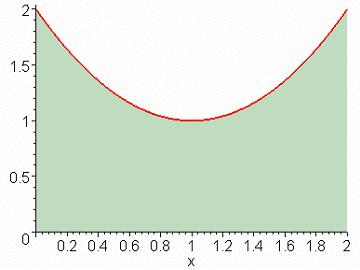
Area under the curve.
Riemann Sums Recap
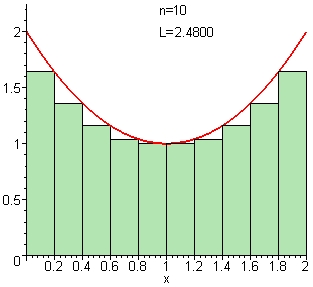
Lower Sum ($m_i$)
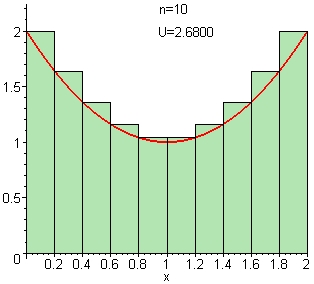
Upper Sum ($M_i$)
$L(f;P) \leq \int_{a}^{b} f(x)\,dx \leq U(f;P)$
The Trapezoid Rule
Instead of rectangles (constant approximation), let's use a linear approximation (Trapezoids).
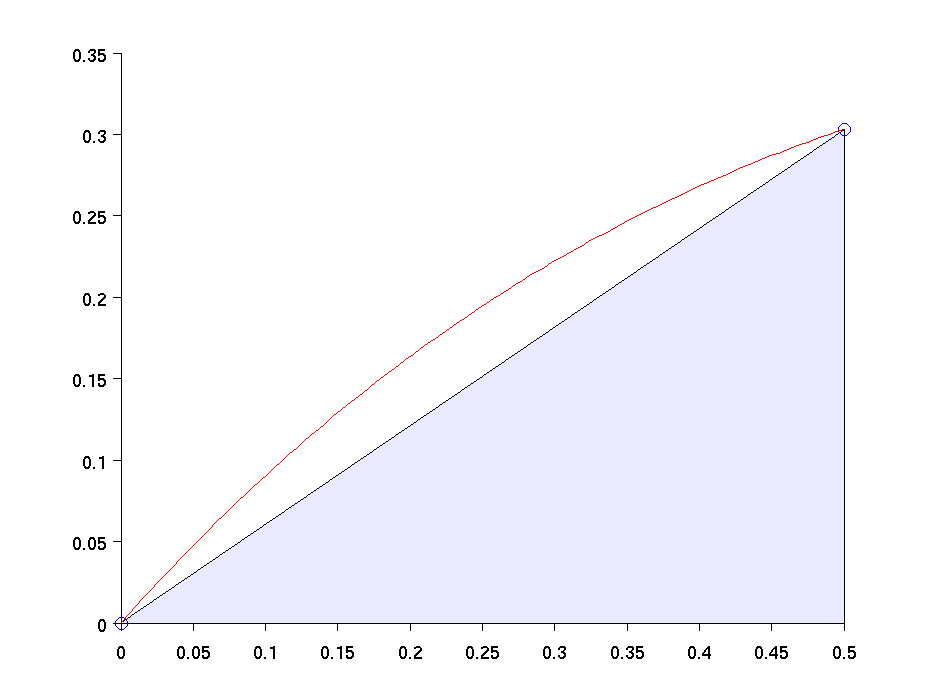
Basic Formula
Area of a trapezoid: avg height $\times$ width.
Composite Trapezoid Rule
Break the interval $[a,b]$ into $n$ sub-intervals of width $h = (b-a)/n$. Apply the trapezoid rule to each.
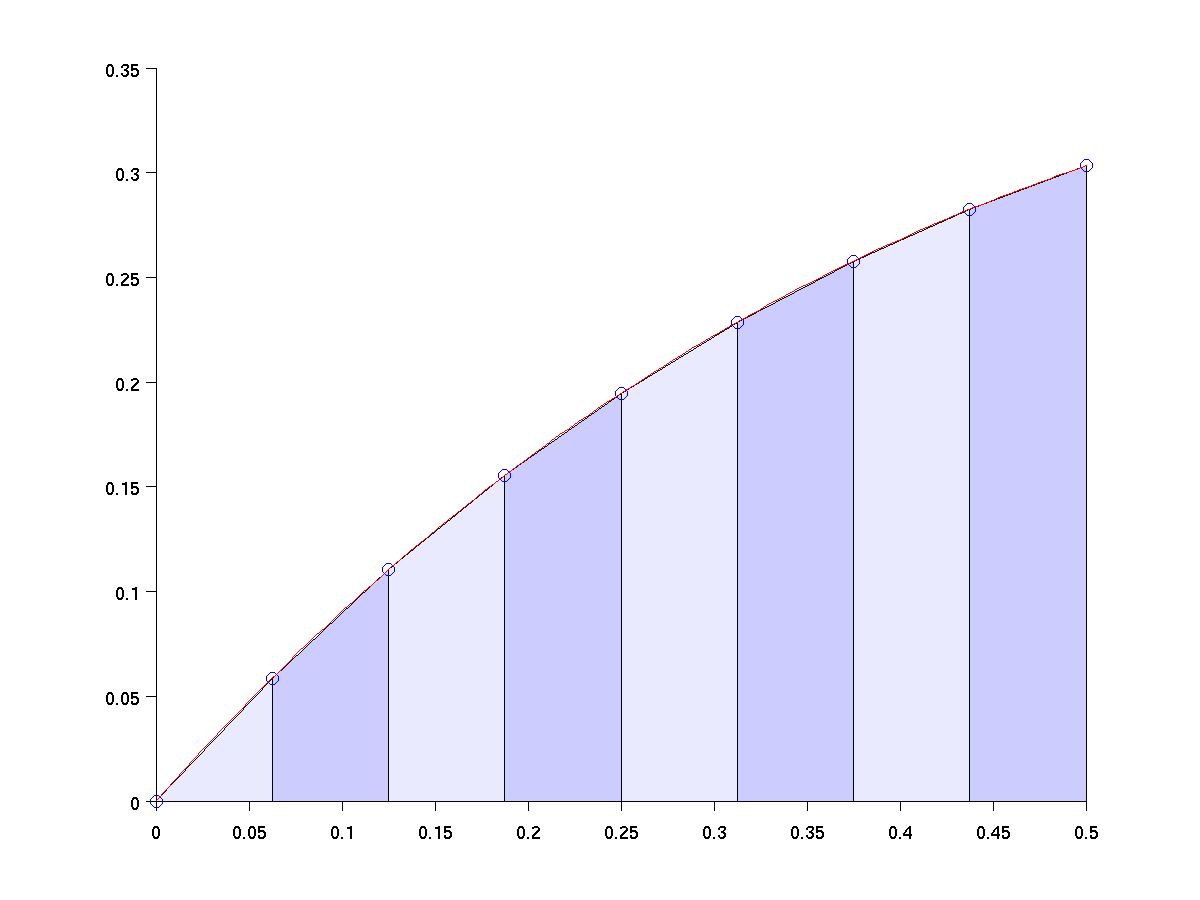
Error Analysis
Error = $-\frac{(b-a) h^2}{12} f''(\eta) = \mathcal{O}(h^2)$
Convergence is quadratic. Halving $h$ reduces error by 4.
Simpson's Rule
Can we do better? Yes, use a Quadratic Approximation (Parabola) over pairs of intervals.
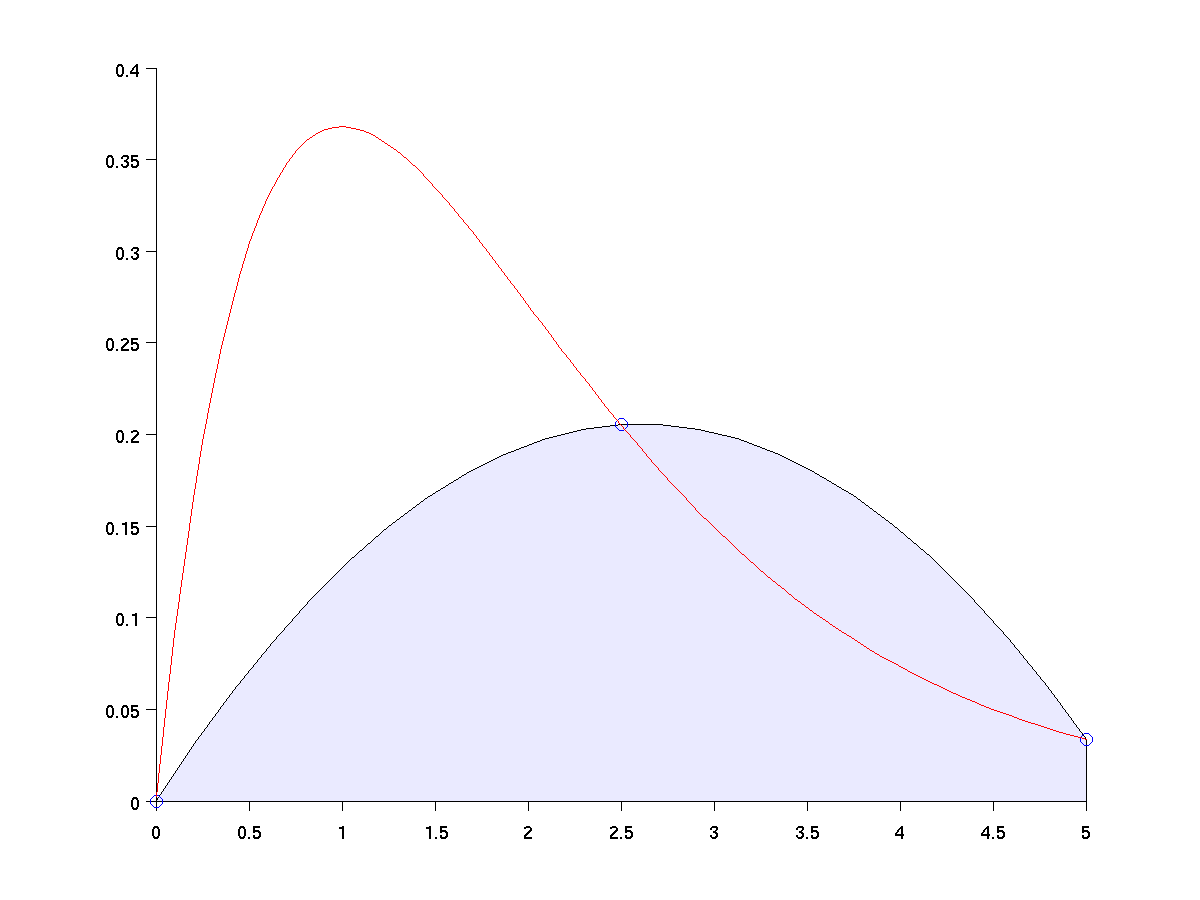
Basic Formula (1/3 Rule)
Requires 3 points (2 intervals of width $h$).
Composite Simpson's Rule
Sum over $n/2$ pairs of intervals.
Error Analysis
Error = $-\frac{(b-a) h^4}{180} f^{(4)}(\xi) = \mathcal{O}(h^4)$
Huge Win: Two orders of magnitude better than Trapezoid!
Newton-Cotes Summary
| Rule | Points ($n$) | Formula | Error Order |
|---|---|---|---|
| Trapezoid | 2 | $\frac{h}{2}(f_0 + f_1)$ | $\mathcal{O}(h^2)$ |
| Simpson's 1/3 | 3 | $\frac{h}{3}(f_0 + 4f_1 + f_2)$ | $\mathcal{O}(h^4)$ |
| Simpson's 3/8 | 4 | $\frac{3h}{8}(f_0 + 3f_1 + 3f_2 + f_3)$ | $\mathcal{O}(h^4)$ |
| Boole's | 5 | $\frac{2h}{45}(7f_0 + 32f_1 + 12f_2 + 32f_3 + 7f_4)$ | $\mathcal{O}(h^6)$ |
🧠 Final Challenge +20 XP
Why does Simpson's Rule generally provide a much better approximation than the Trapezoid Rule for the same step size $h$?