Splines & Bézier Curves
From interpolation to approximation: Creating smooth curves for graphics and data.
Splines: A Quick Review
Linear Spline (Degree 1)
Simply connect the dots.
Continuity: $C^0$ (Value only).
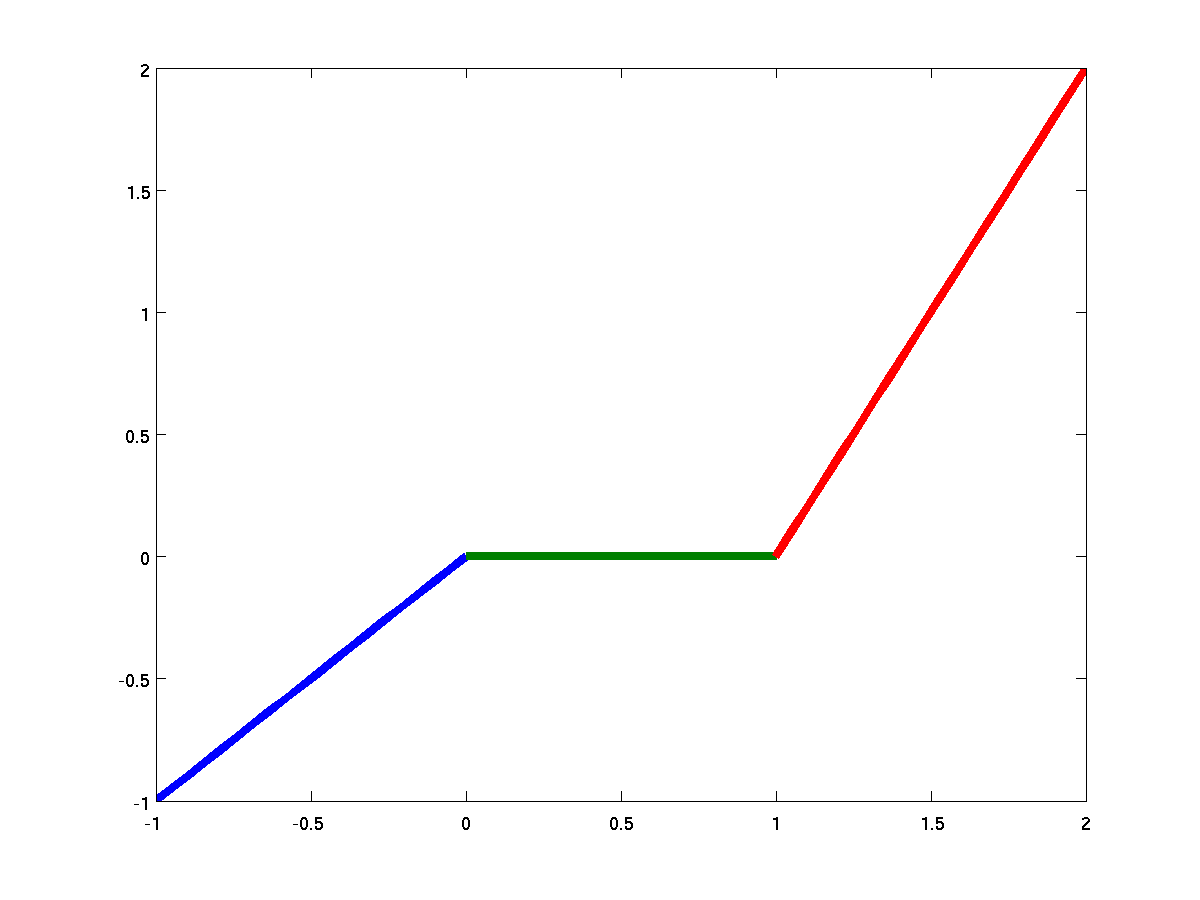
Quadratic Spline (Degree 2)
Parabolas. Requires $S'(x)$ continuity ($C^1$).
One extra constraint needed (e.g., $S'(t_0)$).
Cubic Spline (Degree 3)
The standard for smoothness. Requires $C^0, C^1, C^2$ continuity.
Two extra degrees of freedom. Options: Natural ($S''=0$), Clamped ($S'$ fixed), Not-a-knot.
Natural Cubic Spline Derivation
How do we actually find the coefficients? We solve for the curvatures $z_i = S''(t_i)$.
The Tridiagonal System
Where $b_i = \frac{1}{h_i}(y_{i+1}-y_i)$. Solve for $z$ using $\mathcal{O}(n)$ algorithm!
Bézier Curves
Unlike splines which interpolate (pass through) points, Bézier curves approximate using control points.
- Used in Fonts (TrueType, PostScript).
- Vector Graphics (SVG, Illustrator).
- Curve stays within the convex hull of control points.
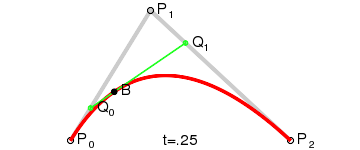
Quadratic (3 Points)
1 Control Point
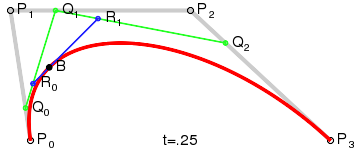
Cubic (4 Points)
2 Control Points
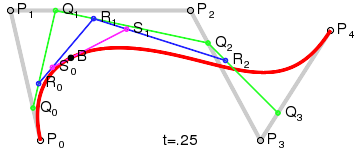
Convex Hull Property
Curve stays inside.
Bernstein Polynomials
Bézier curves are defined parametrically using Bernstein basis polynomials:
$t$ goes from 0 to 1.
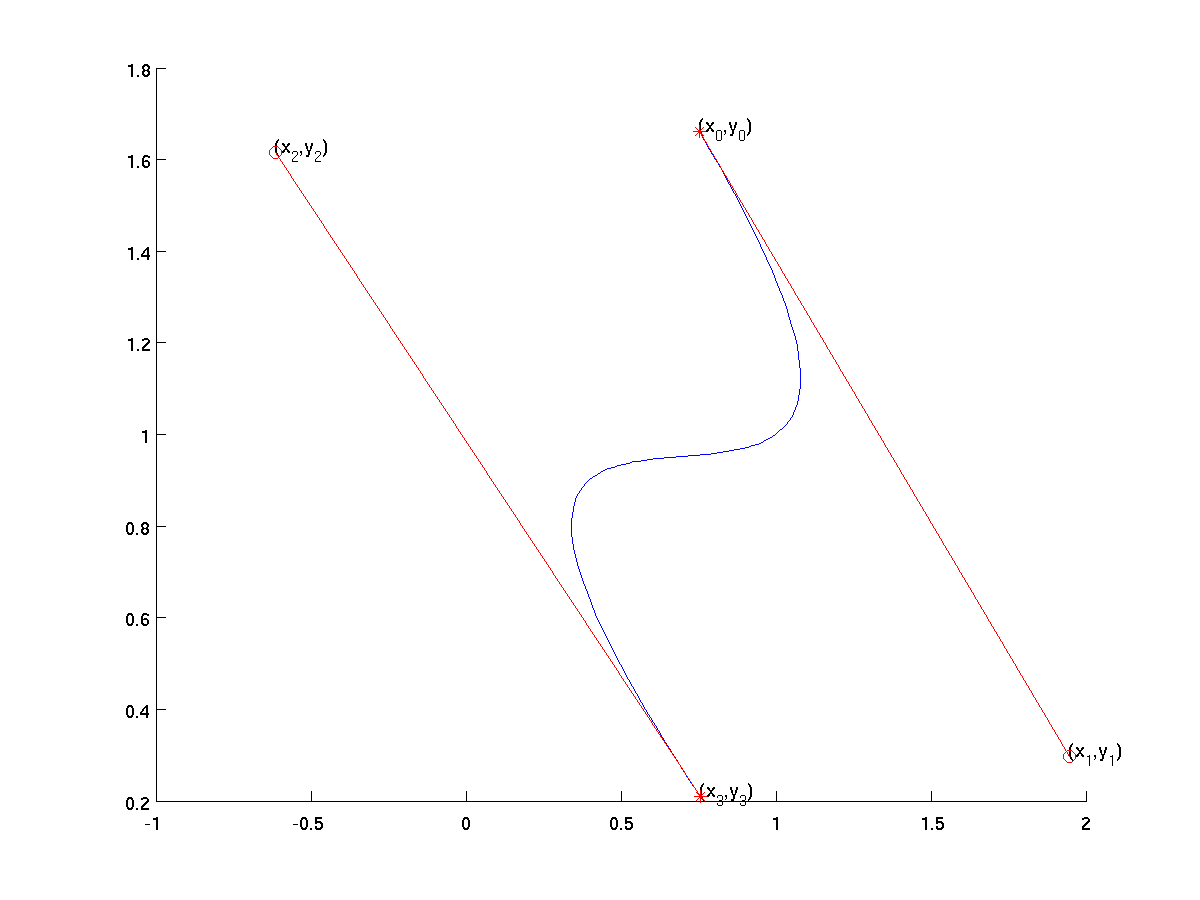
Cubic Bézier ($n=3$)
Uses 4 points: $P_0, P_1, P_2, P_3$.
$y(t) = (1-t)^3 y_0 + 3(1-t)^2 t y_1 + 3(1-t)t^2 y_2 + t^3 y_3$
Key Properties:
- Interpolates endpoints: $P(0)=P_0$, $P(1)=P_3$.
- Tangent at start ($t=0$) is along line $P_0 \to P_1$.
- Tangent at end ($t=1$) is along line $P_2 \to P_3$.
🧠 Final Challenge +20 XP
Which of the following is TRUE about a Cubic Bézier curve defined by points $P_0, P_1, P_2, P_3$?