Interpolation & Splines
From high-degree polynomial oscillations to smooth, piecewise curves.
Polynomial Interpolation Recap
Given $n+1$ points $(x_i, y_i)$, there exists a unique polynomial $p(x)$ of degree $n$ passing through them.
Vandermonde Matrix is ill-conditioned. Expensive.
Stable, but expensive to evaluate ($\mathcal{O}(n^2)$).
Efficient evaluation (Nested Form).
The Problem: Runge's Phenomenon
High-degree polynomial interpolation on equispaced points can oscillate wildly near the boundaries. This is known as Runge's Phenomenon.
Error Bound
$|f(x) - p_n(x)| \leq \frac{M h^{n+1}}{4(n+1)}$
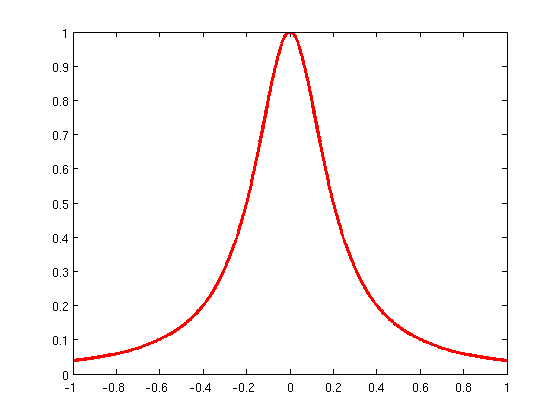
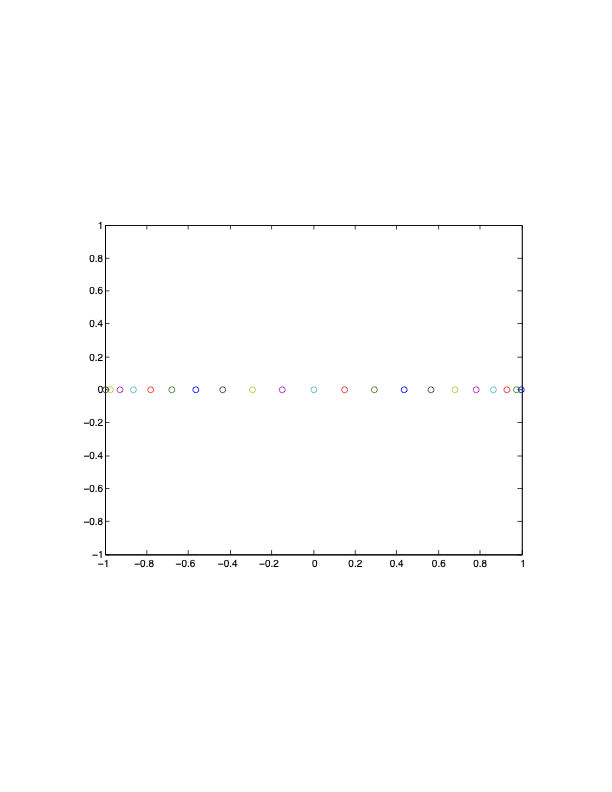
Solution 1: Move Nodes
Use Chebyshev Nodes (clustered near ends). Minimizes the max error.
Solution 2: Piecewise
Don't use one high-degree polynomial. Use many low-degree polynomials connected together (Splines).
Piecewise Polynomials (Splines)
We want curves that are smooth and pass through data points. Used extensively in computer graphics (Fonts, CAD).
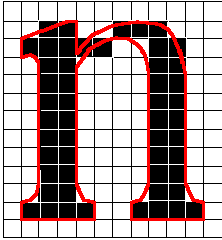

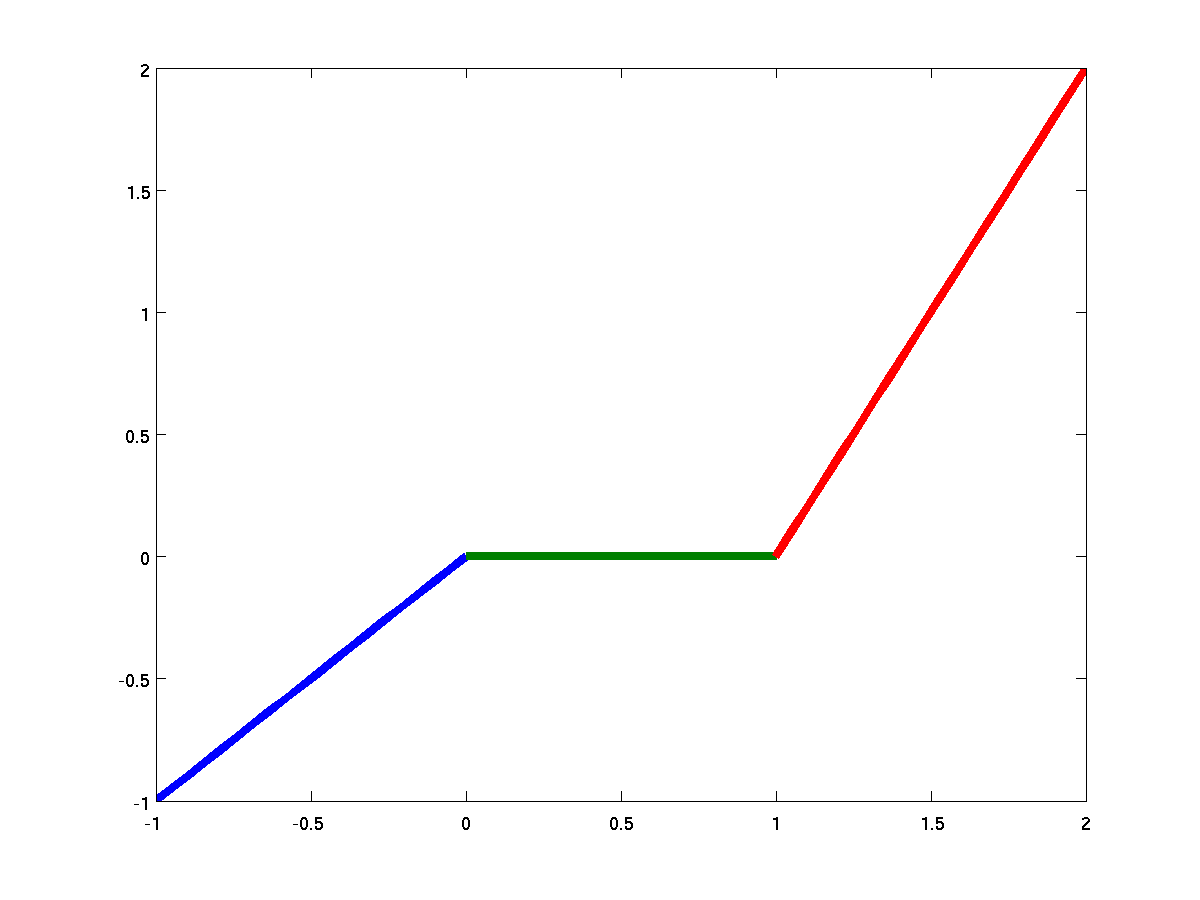
Linear Spline (Degree 1)
Connect points with straight lines.
- Continuous ($C^0$).
- Not smooth (derivative jumps at knots).
- Simple: $S_i(x) = y_i + m_i(x-t_i)$.
Quadratic Spline (Degree 2)
Parabolas on each interval.
- Continuous value ($C^0$).
- Continuous derivative ($C^1$).
- 3 unknowns per interval.
Cubic Splines (Degree 3)
The gold standard for smoothness. Cubic polynomial $S_i(x) = a x^3 + b x^2 + c x + d$ on each interval.
Continuity Requirements
- Value ($C^0$): Curves meet at knots.
- Slope ($C^1$): No sharp corners ($S'$ continuous).
- Curvature ($C^2$): Smooth bending ($S''$ continuous).
Degrees of Freedom
$4n$ unknowns. Constraints leave 2 free parameters.
Common choices: Natural ($S''=0$ at ends), Clamped ($S'$ fixed at ends).
Solving for Coefficients
The problem reduces to solving a Tridiagonal System for the curvatures $z_i = S''(t_i)$.
This system can be solved in $\mathcal{O}(n)$ time!
🧠 Final Challenge +20 XP
Why are Chebyshev nodes preferred over equispaced nodes for global polynomial interpolation?