Roots of Polynomials & Interpolation
Finding zeros of complex polynomials and fitting curves to data points.
Roots of Polynomials
Complications
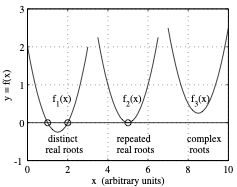
- Repeated Roots: Reduce convergence speed.
- Complex Roots: Require complex arithmetic.
- Sensitivity: Roots can be highly sensitive to small changes in coefficients (Conditioning).
Companion Matrix Method
MATLAB's roots function doesn't use Newton's method. It finds the eigenvalues of a
special matrix!
Interpolation: The Goal
Given $n+1$ points $(x_0, y_0), \dots, (x_n, y_n)$, find a polynomial $p(x)$ of degree $n$ such that $p(x_i) = y_i$.
Uniqueness Theorem
If points $x_0, \dots, x_n$ are distinct, there is a unique polynomial $p(x)$ of degree at most $n$ that interpolates the data.
Monomial Basis
The "obvious" approach: $p(x) = a_0 + a_1 x + \dots + a_n x^n$.
Vandermonde Matrix
Problem: This matrix is often ill-conditioned!
Lagrange Interpolation
Construct the polynomial as a sum of basis functions $\ell_k(x)$ where $\ell_k(x_i) = 1$ if $i=k$ and $0$ otherwise.
Pros
- Conceptually simple.
- No system of equations to solve.
Cons
- Expensive to evaluate ($\mathcal{O}(n^2)$).
- Hard to add a new data point (must recalculate everything).
Newton Form & Divided Differences
The "Smart" approach. Uses a basis that allows for easy updates and efficient evaluation (Horner's method).
Divided Difference Table
Recursive calculation of coefficients $a_k$.
[y1-y0]/[x1-x0]
x1 y1
Interactive Example
Points: $(1,3), (1.5, 3.25), (0,3), (2, 1.67)$
| x | f[] | f[,] | f[,,] |
|---|---|---|---|
| 1 | 3 | ||
| 1.5 | 3.25 | 0.5 | |
| 0 | 3 | 0.16 | 0.33 |
Coefficients are the top diagonal!
🧠 Final Challenge +20 XP
Why is the Newton form often preferred over Lagrange for interpolation?