Nonlinear Equations

The Secant Method

Finding roots without derivatives: A practical alternative to Newton's Method.

⚡ Convergence Recap

Recall that a sequence converges with order $r$ if $\lim_{k\rightarrow\infty} \frac{|e_{k+1}|}{|e_{k}|^{r}} = C$.

Linear ($r=1$)

Adds roughly one digit of accuracy per step (e.g., Bisection).

Quadratic ($r=2$)

Doubles the number of correct digits per step (e.g., Newton's).

1

The Secant Method

Newton's method is great, but calculating $f'(x)$ can be expensive or impossible. The Secant Method approximates the derivative using two previous points.

Derivation

Approximate the derivative:

$f'(x_k) \approx \frac{f(x_k) - f(x_{k-1})}{x_k - x_{k-1}}$

Substitute into Newton's formula:

$x_{k+1} = x_k - f(x_k) \frac{x_k - x_{k-1}}{f(x_k) - f(x_{k-1})}$
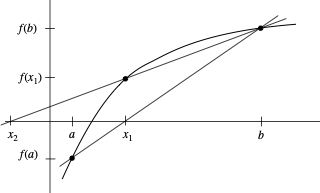
Secant Method Diagram

⚠️ Stability Note

While mathematically equivalent to $x_{k+1} = \frac{f(x_k) x_{k-1} - f(x_{k-1}) x_k}{f(x_k) - f(x_{k-1})}$, using the update form $x_{k+1} = x_k + \Delta$ is better to avoid catastrophic cancellation when $x_k \approx x_{k-1}$.

2

Algorithm & Performance

Secant Algorithm

initialize x1, x2 for k = 2, 3, ... f_k = f(x_k) f_km1 = f(x_{k-1}) if abs(f_k) < tol, stop % Calculate update slope=(f_k - f_km1) / (x_k - x_{k-1}) x_{k+1}=x_k - f_k / slope end

Convergence Comparison

Solve $x - x^{1/3} - 2 = 0$.

k Newton Error Secant Error
1 $4.5 \times 10^{-3}$ $3.5 \times 10^{-3}$
2 $3.8 \times 10^{-7}$ $3.1 \times 10^{-5}$
3 $2.7 \times 10^{-15}$ $2.0 \times 10^{-9}$
4 0.0 $1.3 \times 10^{-15}$

Secant is slightly slower ($r \approx 1.62$) but requires no derivative!

3

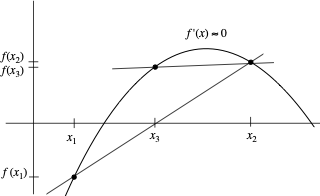
When Secant Fails

Like Newton's method, Secant method assumes the function is locally linear.

  • Flat Spots: If $f(x_k) \approx f(x_{k-1})$, the denominator approaches zero, shooting the next guess to infinity.
  • Poor Guesses: If initial points are not close to the root, it may diverge.
  • No Bracketing: Unlike Bisection, it doesn't guarantee the root stays bracketed.
Secant Failure Diagram
4

MATLAB's fzero

fzero is a robust hybrid solver. It combines the best of all worlds:

🐢
Bisection

Reliable backup if others fail.

🐇
Secant

Fast convergence.

🎯
Inverse Quadratic

Even faster using 3 points.

Reverse Quadratic Interpolation (RQI)

Instead of a straight line (Secant), RQI fits a sideways parabola ($x = ay^2 + by + c$) through three points to find where it hits the x-axis ($y=0$).

RQI Diagram

Usage Example

options = optimset('Display','iter'); f = @(x) x.^10 - 1; [x, fx] = fzero(f, 0.5, options);

🧠 Final Challenge +20 XP

Why might one choose the Secant Method over Newton's Method?