1. Infimum and Supremum
⬇️ Infimum (Greatest Lower Bound)
Let \( S \) be a set of real numbers.
A number \( b \) is a lower bound if \( x \geq b \) for all \( x \in S \).
- If \( b \in S \), it is the minimum.
- If no lower bound exists, \( S \) is unbounded below.
Infimum Definition:
\[ \inf(S) = \text{greatest of all lower bounds} \]⬆️ Supremum (Least Upper Bound)
Let \( S \) be a set of real numbers.
A number \( b \) is an upper bound if \( x \leq b \) for all \( x \in S \).
- If \( b \in S \), it is the maximum.
- If no upper bound exists, \( S \) is unbounded above.
Supremum Definition:
\[ \sup(S) = \text{least of all upper bounds} \]🧠 Quick Check
Consider the set \( S = \{ 1/n \mid n \in \mathbb{N} \} = \{ 1, 1/2, 1/3, \dots \} \)
2. Topology: Interior & Boundary
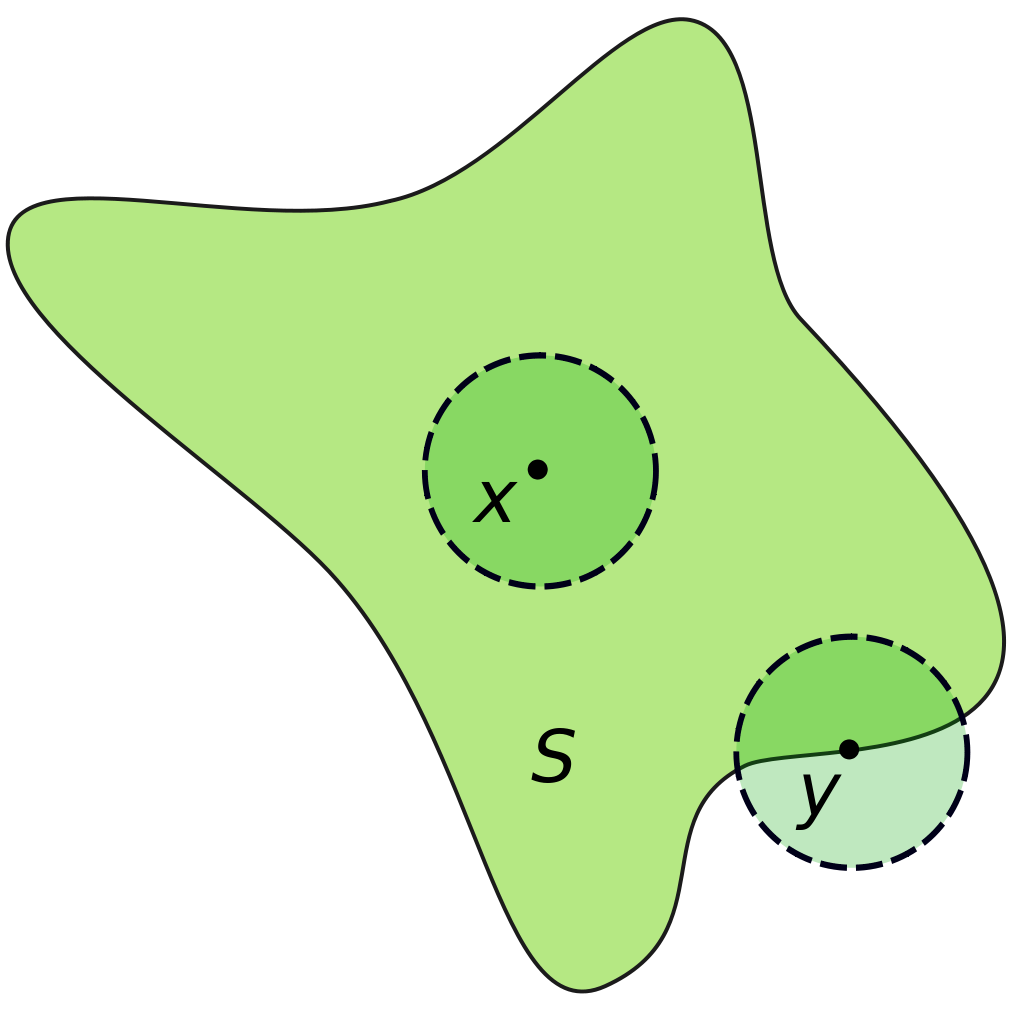
📍 Interior Point
An element \( x \in C \subseteq \mathbb{R}^n \) is an interior point if there exists an \( \epsilon > 0 \) such that a ball centered at \( x \) lies entirely in \( C \):
\[ \{ y \mid \| y - x \|_2 \leq \epsilon \} \subseteq C \]The set of all interior points is denoted \( \textbf{int } C \).
Open Set
A set \( C \) is open if \( \textbf{int } C = C \).
(All points are interior points)
Closed Set
A set \( C \) is closed if its complement \( \mathbb{R}^n \setminus C \) is open.
🚧 Boundary & Closure
- Limit Point: A point \( \ell \) is a limit point if every ball \( B_\epsilon(\ell) \) intersects \( S \).
- Closure (\( \textbf{cl } C \)): The set \( C \) union all its limit points.
- Boundary (\( \textbf{bd } C \)): \[ \textbf{bd } C = \textbf{cl } C \setminus \textbf{int } C \]
3. Test Your Understanding
Which of these are OPEN sets in \( \mathbb{R} \)?
* Click to check. Note: The sine example (4) maps to \( (0, 1] \), which is NOT open because 1 is in the set but 1 is a boundary point!
Find the Interior
\( \{ x \mid -1 \leq x \leq 1 \} \)
(-1, 1)Find the Closure
\( \{ x \mid 1 < x < 2 \} \)
[1, 2]Find the Boundary
\( \mathbb{Q} \) (Rationals)
ℝ (The entire real line!)🔍 Spot the Mistake!
Which statement about open sets is FALSE?