1. What is a Convex Set?
🔷 Geometric Definition
A set is convex if every line segment between two points in the set stays completely inside the set.
Mathematically:
\[ \theta x_1 + (1 - \theta) x_2 \in C, \quad \forall \theta \in [0, 1] \]🔷 Algebraic Definition
Generally, a set is convex if all convex combinations lie in the set:
\[ \sum \theta_i x_i \in C, \quad \text{where } \sum \theta_i = 1, \theta_i \geq 0 \]Visual Comparison
🤔 Quiz: Equivalence
Prove that the geometric definition (2 points) implies the algebraic definition (n points)!
2. Convexity in General Spaces
Maurice Fréchet & Metric Spaces
Metric spaces were first proposed by French mathematician Maurice Fréchet in his 1906 thesis. A metric space is a pair \((X, d)\) where \(d\) is a distance function satisfying:
- \( d(x,y) \geq 0 \) (Non-negativity)
- \( d(x,y) = 0 \iff x=y \) (Identity)
- \( d(x,y) = d(y,x) \) (Symmetry)
- \( d(x,y) \leq d(x,z) + d(z,y) \) (Triangle Inequality)

Maurice Fréchet (1878-1973)
🌐 Menger Convexity
How do we define convexity if we don't have "lines"? Austrian mathematician Karl Menger (1928) proposed using only distance:
A metric space \((X, d)\) is Menger convex if for every distinct \(x, y \in X\), there exists a third point \(z \in X\) such that: \[ d(x,y) = d(x,z) + d(z,y) \]

Karl Menger

Real Projective Space (Boy's Surface)

Morin Surface (Sphere Eversion)
3. Examples of Convex Sets
Hyperplanes & Halfspaces
Hyperplane:
\[ \{ x \mid a^T x = b \} \]Halfspace:
\[ \{ x \mid a^T x \leq b \} \]Intuition: A hyperplane is like a flat sheet (line in 2D, plane in 3D). A halfspace is everything on one side of it.
Hyperplane & Halfspace
Norm Balls
A norm ball is defined as \( \{ x \mid \|x\| \leq 1 \} \). The shape depends on the norm!
L1 Norm (Diamond)
L2 Norm (Circle)
L∞ Norm (Square)
Answer: Yes, for \( p \geq 1 \). For \( 0 < p < 1 \), the "ball" is star-shaped but NOT convex!
Ellipsoids
where \( P \) is symmetric positive definite.
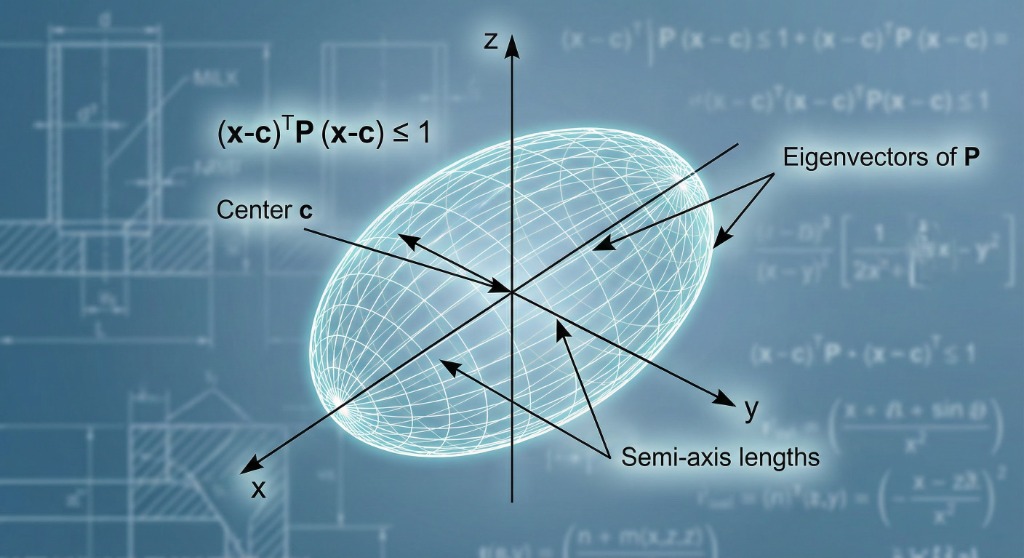
Think of it as a squashed sphere. The eigenvalues of \( P \) determine the axis lengths.
Cones
Norm Cone: \( \{ (x,t) \mid \|x\| \leq t \} \)
Also known as the "Ice Cream Cone" or Second-Order Cone.
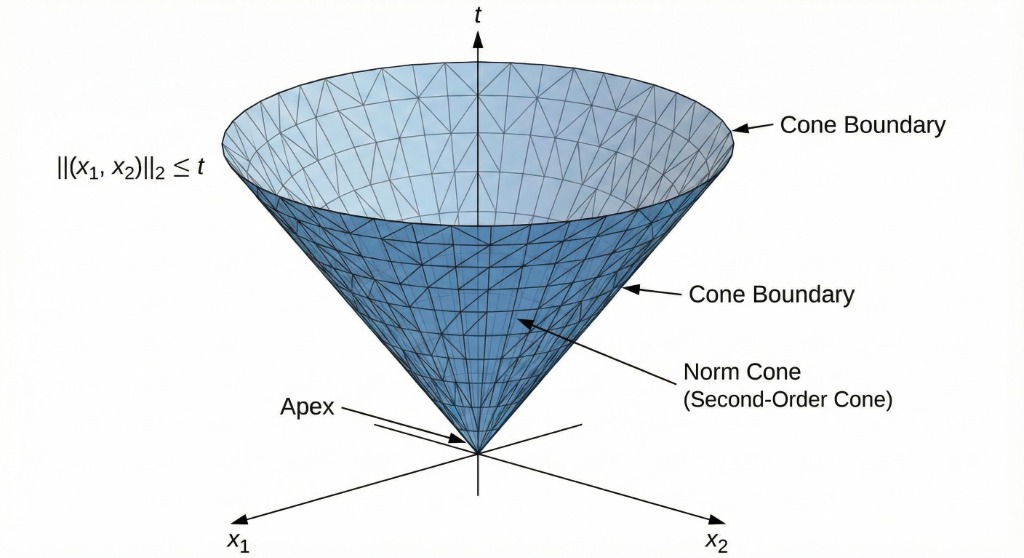
Polyhedra
A polyhedron is the intersection of a finite number of halfspaces and hyperplanes.
\[ P = \{ x \mid Ax \leq b, Cx = d \} \]Note: A bounded polyhedron is called a polytope.

4. Operations Preserving Convexity
1. Intersection
If \( S_1 \) and \( S_2 \) are convex, then \( S_1 \cap S_2 \) is convex.
Generalization: The intersection of any number (even infinite!) of convex sets is convex.
2. Affine Maps
Let \( f(x) = Ax + b \) be an affine function.
- The image of a convex set under \( f \) is convex.
- The inverse image of a convex set under \( f \) is convex.
This means if you stretch, rotate, or translate a convex shape, it stays convex!
Affine map preserves convexity
Examples of Affine Operations
- Scaling: \( \alpha S = \{ \alpha x \mid x \in S \} \) is convex.
- Translation: \( S + a = \{ x + a \mid x \in S \} \) is convex.
- Projection: The shadow of a convex object is convex!
🔍 Spot the Mistake!
Find the error in this statement about unions:
1. The intersection of two convex sets is always convex.
2. A single point is a convex set.
3. The union of two convex sets is always convex.