1. Introduction to Forecasts
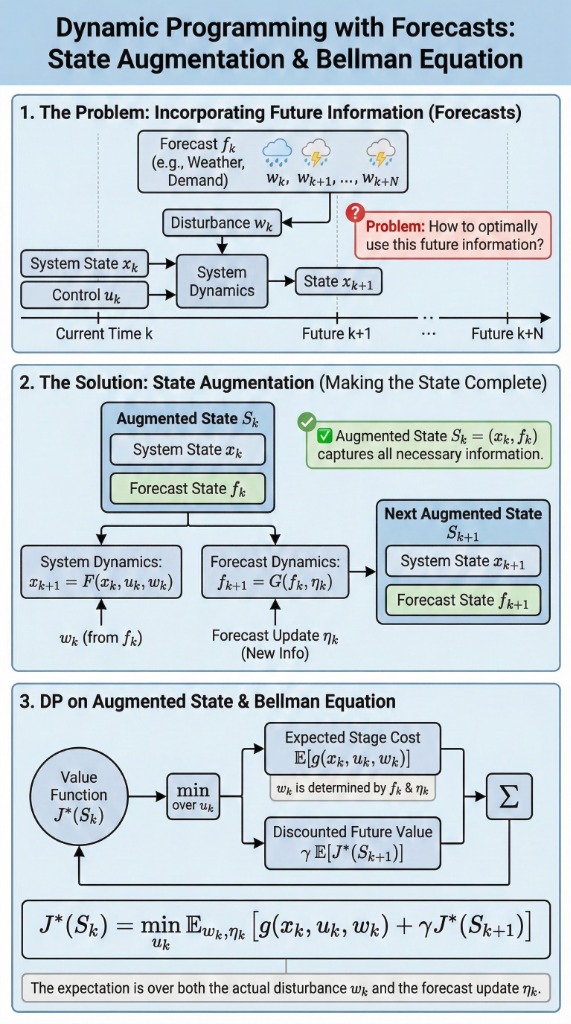
At time \(k\), the controller receives a forecast \(y_k\). This forecast changes our belief about the upcoming disturbance \(w_k\).
Weather
Rain probability affects agriculture decisions.
Interest Rates
Economic forecasts affect investment.
Demand
Inventory needs based on market trends.
Forecast Model
If the forecast is \(y_k = i\), then the disturbance \(w_k\) is selected according to a specific probability distribution \(P_i\).
2. The Forecasting Equation
The forecast itself evolves over time:
\[ y_{k+1} = \xi_k \]Where \(\xi_k\) is a random variable representing the next forecast.
Forecast Evolution
3. Augmented System
We combine the physical system state \(x_k\) and the information state (forecast) \(y_k\) into a new augmented state.
Augmented State Definition
\[ \tilde{x}_k = \begin{bmatrix} x_k \\ y_k \end{bmatrix}, \quad \tilde{w}_k = \begin{bmatrix} w_k \\ \xi_k \end{bmatrix} \]The system dynamics become:
\[ \tilde{x}_{k+1} = \begin{bmatrix} f_k(x_k, u_k, w_k) \\ \xi_k \end{bmatrix} \]Augmented System Diagram
4. DP Algorithm with Forecast
The DP algorithm is applied to the augmented state \((x_k, y_k)\).
Bellman Equation
\[ J^*_k(x_k, y_k) = \min_{u_k} E_{w_k} \left\{ g_k(x_k, u_k, w_k) + \sum_{i=1}^{m} p_i J^*_{k+1}(f_k(x_k, u_k, w_k), i) \mid y_k \right\} \]Note: The expectation \(E_{w_k}\) depends on the current forecast \(y_k\).
5. Summary Infographic
6. Test Your Knowledge
1. A forecast \(y_k\) primarily affects:
2. The "Forecasting Equation" \(y_{k+1} = \xi_k\) implies:
3. In the augmented state \(\tilde{x}_k = (x_k, y_k)\), the variable \(y_k\) is:
4. The DP algorithm expectation is conditional on:
5. Can forecasts be influenced by control actions?
🔍 Spot the Mistake!
Scenario 1:
"The forecast \(y_k\) is always a perfect prediction of \(w_k\)."
Scenario 2:
"We can solve the problem without augmenting the state with \(y_k\)."
Scenario 3:
"The next forecast \(y_{k+1}\) depends on the current disturbance \(w_k\)."