1. Introduction
Tetris can be modeled as a finite horizon stochastic DP problem with a very long horizon.
2. State Formulation
The state consists of two primary components:
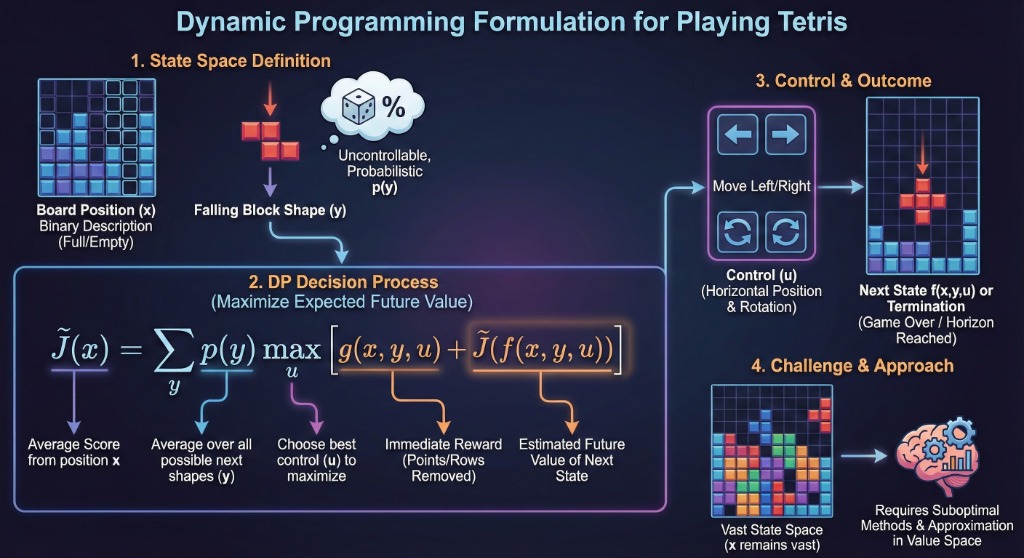
1. Board Position (\(x\))
A binary description indicating whether each square is full or empty.
2. Falling Block Shape (\(y\))
The shape of the currently falling block (e.g., L-shape, Square).
Control (\(u\)): Determines the horizontal position and rotation applied to the falling block.
3. DP Algorithm
The shape \(y\) is generated by a probability distribution \(p(y)\) and is independent of the control. It is an uncontrollable state component.
Reduced Bellman Equation
We can average out \(y\) to define \(\tilde{J}(x)\), the "average score" at position \(x\):
\[ \tilde{J}(x) = \sum_y p(y) \max_u \left[ g(x, y, u) + \tilde{J}(f(x, y, u)) \right] \]
Where:
- \(g(x, y, u)\): Points scored (rows removed).
- \(f(x, y, u)\): Next board position.
4. Remarks
Tetris has been a compelling platform for RL research (1995-2015).
- The state space \(x\) is vast (astronomical number of board configurations).
- Exact DP is impossible; suboptimal methods and approximation in value space are required.
- Notable works: [TsV96], [BeI96], [BeT96], [GGS13], [SGG15].
5. Test Your Knowledge
1. The state in Tetris consists of:
2. Which component is uncontrollable?
3. The value \(\tilde{J}(x)\) represents:
4. Why do we need approximation methods for Tetris?
5. The immediate reward \(g(x,y,u)\) is typically:
🔍 Spot the Mistake!
Scenario 1:
"We can control the next block shape by playing well."
Scenario 2:
"The reduced Bellman equation eliminates the need for maximization."
Scenario 3:
"Tetris is a deterministic shortest path problem."