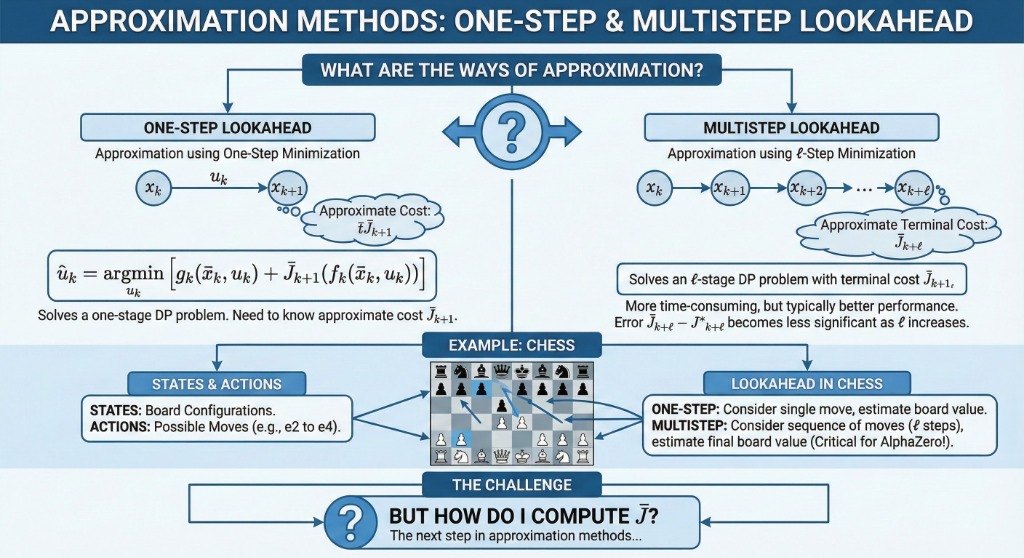
1. Ways of Approximation
We've established that we need to approximate the optimal cost-to-go function \( J^* \). But how far should we look ahead before applying this approximation?
One-Step Lookahead
Look one stage ahead, then approximate.
Multistep Lookahead
Look \( \ell \) stages ahead, then approximate.
2. One-Step Lookahead
Definition
The algorithm involves a one-step lookahead minimization if it solves a one-stage DP problem for each \( k \):
\[ \tilde{u}_k = \arg\min_{u_k \in U_k(\tilde{x}_k)} \left[ g_k(\tilde{x}_k, u_k) + \tilde{J}_{k+1} (f_k(\tilde{x}_k, u_k)) \right] \]- At state \( k \), you look ahead to various possible next states \( x_{k+1} \).
- Minimization is performed over controls \( u_k \).
- We require the approximate cost \( \tilde{J}_{k+1} \).
3. Multistep Lookahead
Multistep lookahead involves solving an \( \ell \)-step DP problem, where \( 1 < \ell < N - k \), with a terminal cost function approximation \( \tilde{J}_{k+\ell} \).
Why use Multistep?
It typically provides better performance. The intuitive reason is that by treating \( \ell \) stages "exactly" via optimization, the effect of the approximation error \( \tilde{J}_{k+\ell} - J^*_{k+\ell} \) tends to diminish as \( \ell \) increases.
Example: In AlphaZero chess, long multistep lookahead is critical for superior performance.
Trade-off:
The solution becomes more time-consuming compared to one-step lookahead.
4. Example: Chess
Analyzing the Game
-
?
States:
The arrangement of pieces on the board.
-
?
Actions (Controls):
Legal moves available to the current player.
-
?
Lookahead:
Calculating potential future board states. Grandmasters might look 10-15 steps ahead (Multistep), while novices might only look 1 step ahead.
But how do I compute \( \tilde{J} \)?
We've talked about using \( \tilde{J} \) for approximation, but we haven't discussed where this function comes from.
Find out in the next lecture →