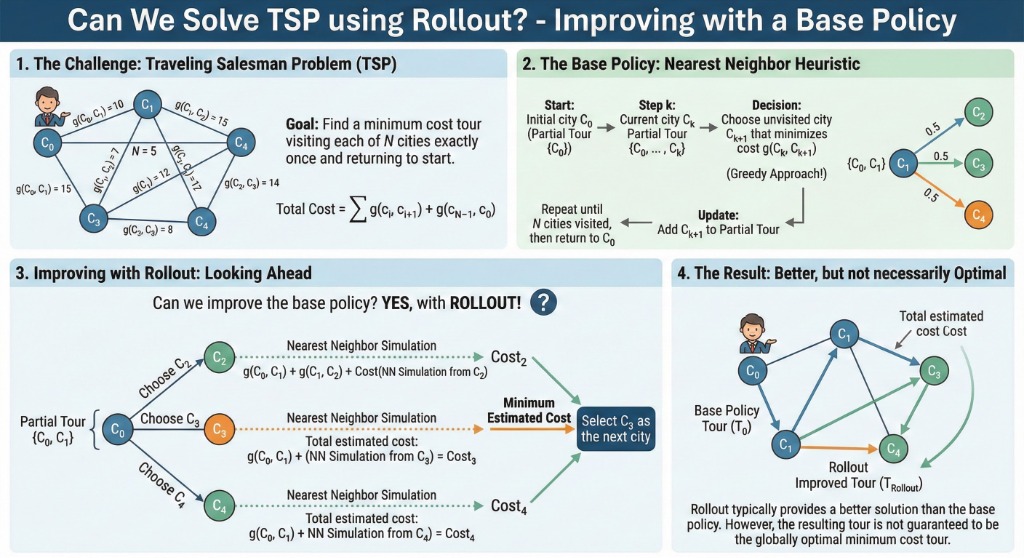
1. The Traveling Salesman Problem (TSP)
Recall the classic problem: A salesman wants to find a minimum cost tour that visits each of \( N \) given cities \( c = 0, \dots, N - 1 \) exactly once and returns to the start.
Key Components
- Cities: \( N \) cities.
- Cost: \( g(c, c') \) is the traversal cost between distinct cities \( c \) and \( c' \).
- Connectivity: Assume full connectivity (use high cost for non-existent links).
- Goal: Find a visit order with minimum total cost.
2. A Base Policy for TSP
To use rollout, we need a base policy. A common and simple heuristic is the Nearest Neighbor heuristic.
Nearest Neighbor Heuristic
This heuristic constructs a tour greedily:
- Start with an initial partial tour (e.g., just the starting city \( c_0 \)).
- Given the current city \( c_k \), choose the next city \( c_{k+1} \) that minimizes the cost \( g(c_k, c_{k+1}) \) among all unvisited cities.
- Repeat until all \( N \) cities are visited and return to \( c_0 \).
Total Heuristic Cost = \( g(c_0, c_1) + \dots + g(c_{N-2}, c_{N-1}) + g(c_{N-1}, c_0) \)
3. Improving with Rollout
Given that we have a base policy, can we improve it? Yes, with Rollout!
The Process
At each step of constructing the tour:
- Consider all possible next cities (controls).
- For each candidate next city, run the Nearest Neighbor heuristic to complete the tour.
- Calculate the total cost (immediate step + heuristic completion).
- Choose the next city that results in the lowest total estimated cost.
4. Comparison: Base vs. Rollout
| Method | Description | Performance |
|---|---|---|
| Base Heuristic (T0) | Nearest Neighbor: Always pick the closest unvisited city. | Fast, but often suboptimal (greedy). |
| Rollout (T1) | Look one step ahead, then use Nearest Neighbor to estimate the rest. | Slower, but typically finds a much better tour. |
* Note: Rollout is not guaranteed to find the optimal solution, but it reliably improves upon the base heuristic.